
Appropriate scale-up/down is key for further larger production. Important is to focus to the right parameters that can help us to set the design for all experiments at lab scale.
The common approach within the up-stream processing (USP) part in biologics is to increase the scale 10 times. It means from e.g. 25L lab scale to max. 250L pilot scale and later on from pilot scale to max 2500L production scale. Key parameters are vessel geometry, agitation, aeration, back-pressure and feeding profiles (in case of fed-batch fermentation). Next diagram shows typical construction of a common fermenter with key parameters:
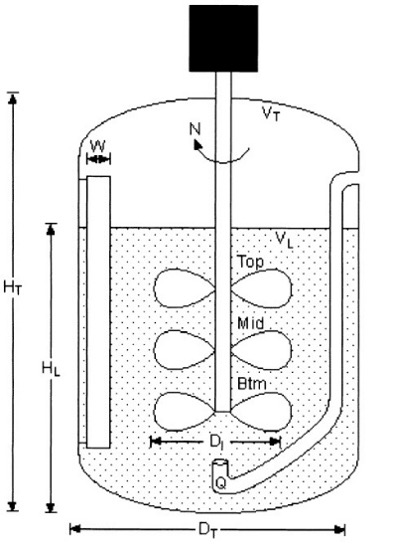
Geometric similarity of fermenter geometry is a pre-requisite for applying established scale-up relationship. It´s expressed as follows: DT2/DT1 = (VT2/VT1)1/3, where DTi is fermenter diameter and VTi total fermenter volume. Geometric similarity also assumes reasonably constant impeller geometry such as impeller diameter (DI) and number of impellers (N). Based on target total a/o working volumes obtained from geometric similarity, the desired working volume in the fermenter may be altered during experimentation. The ratio of the impeller to fermenter diameter (DI/DT) in standard fermenters is between 0.3 to 0.45. Fermenters with a standard geometry are beneficial within scale-up correlations assuming constant geometry. Common pilot scale-up fermenters have HT/DT ratios of 3:1, but they can also decrease to 1:1.
The first approach within agitation is to check the design of impellers, number of impellers, diameter and location. Common impellers used within microbial fermentations are Rushton turbines or Hollow-blade (U-shape), but could also be Hydrofoil, Maxflo, etc. Stirrer tip speed (STS) is the simplest approach normally used in case of same design of impellers between two scales. It is formulated as STS = πNIDI, where π is a constant, NI and DI are the impeller speed (s-1) and impeller diameter (m) in fermenter respectively. Typical STS ranges from 3.8 to 7.6 m/s.
More complex approach within agitation is Constant (gassed) power input per liquid volume (PG/VL) which characterizes energy generated by impeller to liquid volume used in the fermenter. It is normally used in a case of scale-up for various design of impellers between two scales. PG/VL is expressed as PG/VL = P0/VL*0.5 = ((NPNI3DI5ρ)/VL)*0.5, where NP is the power number, which means proportionality factor based on impeller design (NP for Rushton is 5 and for Hollow-blade is 1.5). NI and DI are the impeller speed (s-1) and impeller diameter (m), ρ is specific broth density (kg/m3) and VL is volume of fermentation broth (L). General values of PG/VL in large scale (fermenter with a total volume more than 1500L) are between 1 to 3 W/L. It´s difficult to have high power per unit volume at the large scale due to practical limitation of the motor size.
Additional scale-up parameters are focused to oxygen transfer. They are Oxygen Uptake Rate (OUR) and Mass transfer coefficient (KLa). Scale-up based on OUR assumes that the OUR is equal to Oxygen transfer rate (OTR). This equation is expressed as OTR = KLa(csat – cL) = OUR = μX/YX/O2 , where csat is the broth dissolved oxygen (DO) at saturation, cL is the measured broth DO concentration, μ is the specific growth rate, X is the measured cell density and YX/O2 is the cell yield calculated per amount of consumed oxygen. There are several correlations for the determination of KLa using Gassed power per liquid volume (PG/VL) described previously and Superficial gas velocity VS, where the formula looks is KLa = f2(PG/VL)aVSb , where f2 is a proportionality constant. In general, the “a” value within this equation decreases with increasing working volume. The “a” value is 0.95, 0.67 and 0.5 for fermenters from lab scale (e.g. 10L scale), pilot scale (300L) and production scale (more than 20,000L) respectively. Same holds for the “b” value: 0.67 for lab and pilot scale and 0.50 for production scale. The formula for Superficial gas velocity (VS) is VS = φG/(π/4)*DI2), where φG is Gass flow rate (m3/s) and DI is impeller diameter (m). Finally Gass flow rate can be calculated using φG = (Q * (tact/t0)*(Patm/Pabsolute))/3600, where Q is airflow rate (Nm3/s), tact and t0 are actual temperature and temperature of absolute ZERO in Kelvin and finally Patm and Pabsolute are the pressures. Production fermenters up to 100,000L scale have KLa value between 400 to 800 h-1. Scale-up based on KLa is complicated approach by the fact that it is process specific and it changes over the fermentation, making it difficult to reliably quantify. Alternatively, measurement of broth DO concentration (CL) can be used as an adequate scale-up parameter. The minimum acceptance value of CL is well known from lab scale experiments. Cascade control of DO by agitation, aeration and back-pressure can be effective in maintaining of DO above critical value.
The Table 1 shows an example of most important parameters within scale-down model from 300L pilot fermenter to 75L lab fermenter. Appropriate set of all required parameters in small scale can be predictive for consecutive production in large scale. Finally, all set process parameters need to be confirmed in larger scale via pilot or ENG/Validation batches within further cGMP production.
CMC experts from Venn Life Sciences have strong expertise within theoretical and practical application of these models. Do you need more insight or support with your up-scaling process? Do not hesitate to contact us via our website: www.vennlifesciences.com.
Table 1. Practical application of scale-down model from pilot fermenter (300L) to laboratory fermenter (50L).
| 300L pilot fermenter | Fermenter parameters used for Scale down | 75L lab. fermenter |
| 3.32 | Ratio HT/DT | 3:1 |
| 200L | Working volume Vmax | 50L |
| Rushton, 3 times | Impeller type and No. | Rushton, 3 times |
| 0.23 | Impeller diameter DI | 0.12 |
| 4 kW | Engine power PE | 1.1 kW |
| 22 kW/m3 | Engine input per working volume PE/VL = PE/(Vmax/1000) | 20 kW/m3 |
| 420 rpm = 7 rps | Agitation Nmax | 800 rpm = 13.33 rps |
| 5.06 | Stirrer tip speed STSmax = πNmaxDI | 5.03 |
| 16.8 Nm3/h = 280 L/min | Airflow rate Qmax | 6 Nm3/h = 100 L/min |
| 1.40 vvm (1/min) | Volumetric airflow rate per volume Qmax/Vmax | 2 vvm (1/min) Scale down recalculation to 1.4 vvm corresponds to airflow 70 L/min |
| 5.15 W/L (for Nmax) | Constant (gassed) power input per liquid volume P0/VL*0.5 = ((NPNI3DI5ρ)/VL)*0.5 | 5.50 W/L (for Nmax) Scale-down recalculation to 5.15 W/L corresponds to agitation 782 rpm |
Note: For successful scale down model is necessary to set appropriate parameters in lab. scale such as agitation, aeration and back-pressure, that mimic parameters in pilot scale.
Date: 24.10.2022
Author: Juraj Boylo